一致性入门之--RAFT论文理解
RAFT 是为了保证一致性的工程实现方法。其想法来自于Paxos,由于Paxos极其难以理解以及高复杂性,在工程上实现难度异常大。Diego Ongaro 和 John Ousterhout 提出了一种便于理解和工程实现的一致性算法,其复杂程度相比于raft要低很多,因而使得该一致性算得到了更好的普及。
何为一致性算法?
个人理解一致性算法是为了解决分布式系统中,各个子部分对于某一个共同过程所达成的共识。在分布式存储理论中有一个非常有名的理论CAP theory。当然该理论的重点不在一致性,有兴趣的同学自行google。这里借用CAP theroy对于一致性的定义,也就是所谓的C(consensus)。
在CAP theory, Wikipedia 的解释
Consensus:Every read receives the most recent write or an error.
在一个存储系统中,在同一时间,每一次读一定是一样的最新的数据或者读到一个error。
为什么需要一致性算法?
在存储系统当中,这个问题的第一反应一定是为了保证数据的一致性。更具挑战的是保证在故障频繁发生的条件下保证数据的一致性。对于一个完整的存储系统,存储节点的单点故障应该是常态。对于三副本系统来说,保证大多数的副本存活(两副本存活)就可以保证数据的一致性,这也解决了单点故障的问题。
RAFT论文
角色:
Leader:负责client端的请求,并发送到其他follower上,处理与follower的同步。
Follower:负责接收Leader的副本,可以看作leader的备份。
Candidate:在投票阶段存在的角色,负责将自己的投票发送出去,同时处理收到的投票。
Overview:
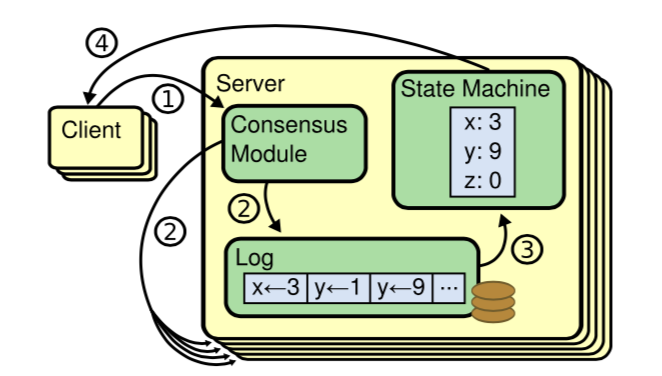
可以看到抽象的系统流程如上图所示。client将请求发送到leader上,leader负责将副本发送到其他follower上,在收到大多数的follower回复之后,将这个log同步到state machine上。最后返回客户端。
Raft论文主要论证了Raft会保证一下的性质:

Election Safety:每个时间片(term)内最多选出一个leader
个人理解,由于raft是一个大多数的游戏,任何candidate在获得了大多数的投票之后就会变成leader,所以在一组candidates中只能最多有一个candidate拿到大多数选票,既只能最多有一个leader。
Leader Append-Only:leader只能添加新的entries不能删除或者重写。
个人理解,要注意这里是leader的限制。由于raft算法中strong leader的特性,leader对于follower的log有绝对的主导权。也就是说follower的log是可以由leader改变的。
Log Machine:如果两个log 有相同的index 和term,他们之前的所有log 一定相同。
个人理解,这是一条非常重要的特性,对于后边的safety证明(leader拥有所有committed entries)有重要的作用。为了保证这一特性,在主从同步log的时候,主会带着当前同步点之前一个序号的log信息(假设A),从需要拥有这一条log才能接受当前的主同步的index为A+1的log。以此类推,主从同步点之前的log一定是相同的。
Leader Completeness:提交的committed的log一定会一直存在下去。
个人理解,新主一定会拥有之前所有提交的committed的log。这里比较抽象,具体的证明在5.4.3小节,有兴趣的同学强烈建议读原文。简而言之,每一次选主的时候由于选择的是拥有更大的term或者更长的log的candidate。每一次即使有candidate宕机重启,也会选出大多数中拥有那次committed的那个candidate。当然如果半数以上的candidate都宕机了,那根本没有一致性可言了,不是raft考虑的范围之内。
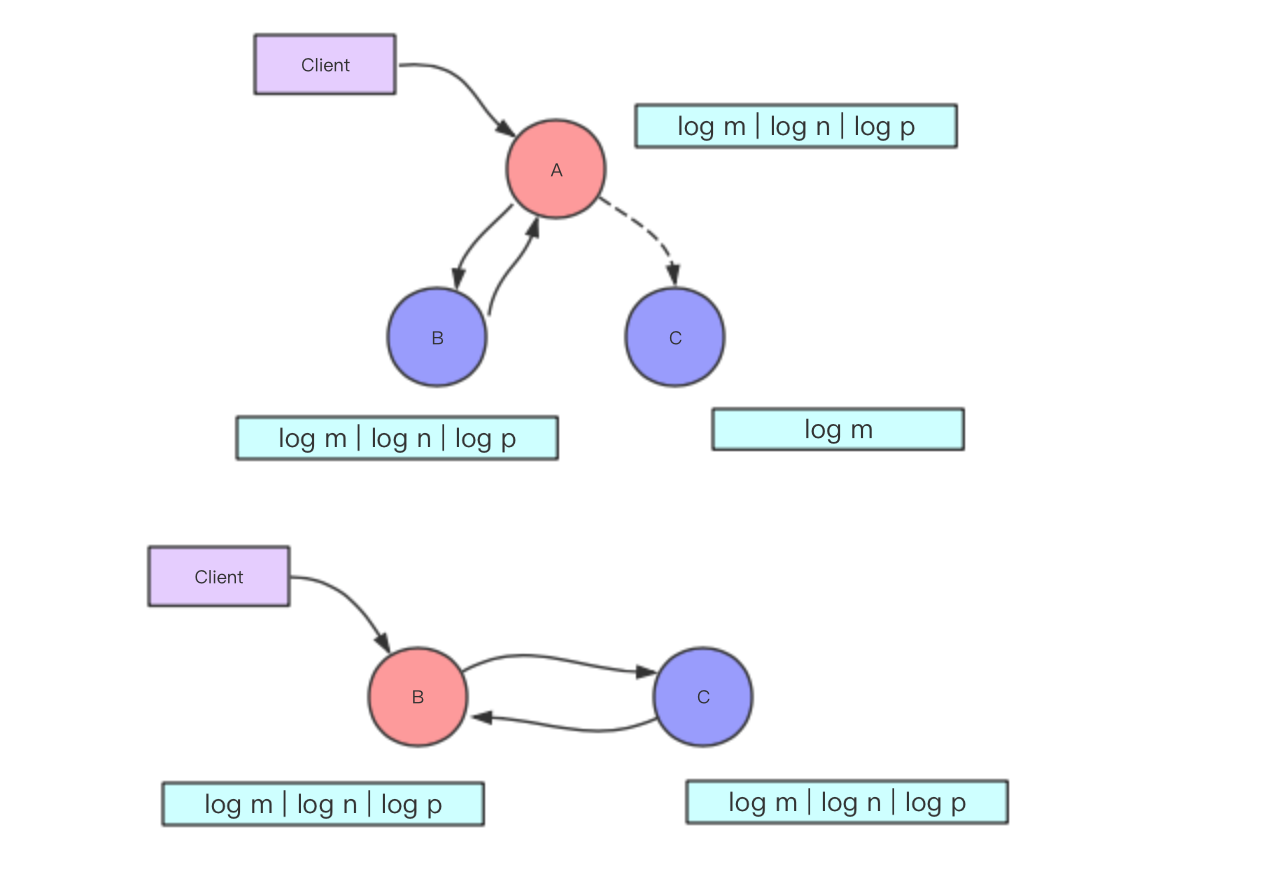
如上图所示A为leader,B,C为follower。A收到B的(大多数)response 的时候就会commit log n以及log p。这时候如果A 宕机,B由于拥有更长的log选为新的leader,这时候会将log 同步给C完成log的复制。
运用以上性质raft论文讨论了三个问题
- Leader Election
- Log Replication
- Safety
对于问题1,RAFT给出了极其详细的工程实现,具体流程参考 RAFT流程概述。在接下来的博客中会结合RAFT优秀实现FLOYD 源码对问题1 进行详细的讨论。敬请期待。